Improving Fluency and Number Sense with Simple Number Exercises
There is often a debate about striking the perfect balance between computational fluency (think: basic facts and algorithms) and number sense (think: comparing, ordering, and estimating values). Experience and research indicates that number fluency is as important as number sense, and that each one depends, in part, on the other. If children have a degree of fluency, they can reduce the chance of cognitive overload when tackling more demanding challenges.
As educators, we have to take care not to create an either or situation. It is probably more healthy to think of the concept o “flexible numeracy.” This is an approach where a student is given the opportunity to tackle both approaches and move between the two seamlessly.
As a math teacher, I try to think of my students as number athletes. I want them to be able to slip effortlessly between and around exercises; with operations; bounce from strategy to strategy with ease. Just as athletes stretch every day, with purpose and dedication, students who wish to be flexible with numbers must stretch their numerical skills daily. My role, for five minutes a day, becomes that of a fitness coach, guiding my students enthusiastically in a brief stretching exercise, to keep them nimble with numbers.
The exercises themselves are simple: since the objective is strictly to practice manipulating numbers, there is no need to come up with real-world contexts. (Problem-solving is embedded throughout the rest of the math lesson.) But don’t let the simplicity of the exercise fool you: as they contemplate solutions, students’ minds flow through a range of interrelated number concepts: the relationship between addition and subtraction, the pairs that make ten, ordering numbers on the number line, conservation of number, and plenty more. They are building fluency while exercising number sense; they are accessing number concepts while practicing basic facts. In short, they are becoming numerically flexible.

Home
We speak to Geoff Barton to explore the Oracy Commission Report: We need to talk, and its significance for maths teaching
Home | NZMaths
The Ministry of Education has migrated nzmaths content to Tāhūrangi. e-ako maths or e-ako Pāngarau along with e-ako PLD 360 are still available. Navigate there by choosing the option below. You may need to update your nzmaths account the first time you log in to e-ako.
http://www.doe.mass.edu/sfss/math-protocols/
[embedyt] https://www.youtube.com/watch?v=LkrfZ0Y-V2I[/embedyt]
Highlights of our summer conference in Uttoxeter, 2016 with mastery of mathematics as a key theme. With special thanks to Jane Jones (HMI) and Debbie Morgan (NCETM primary director).
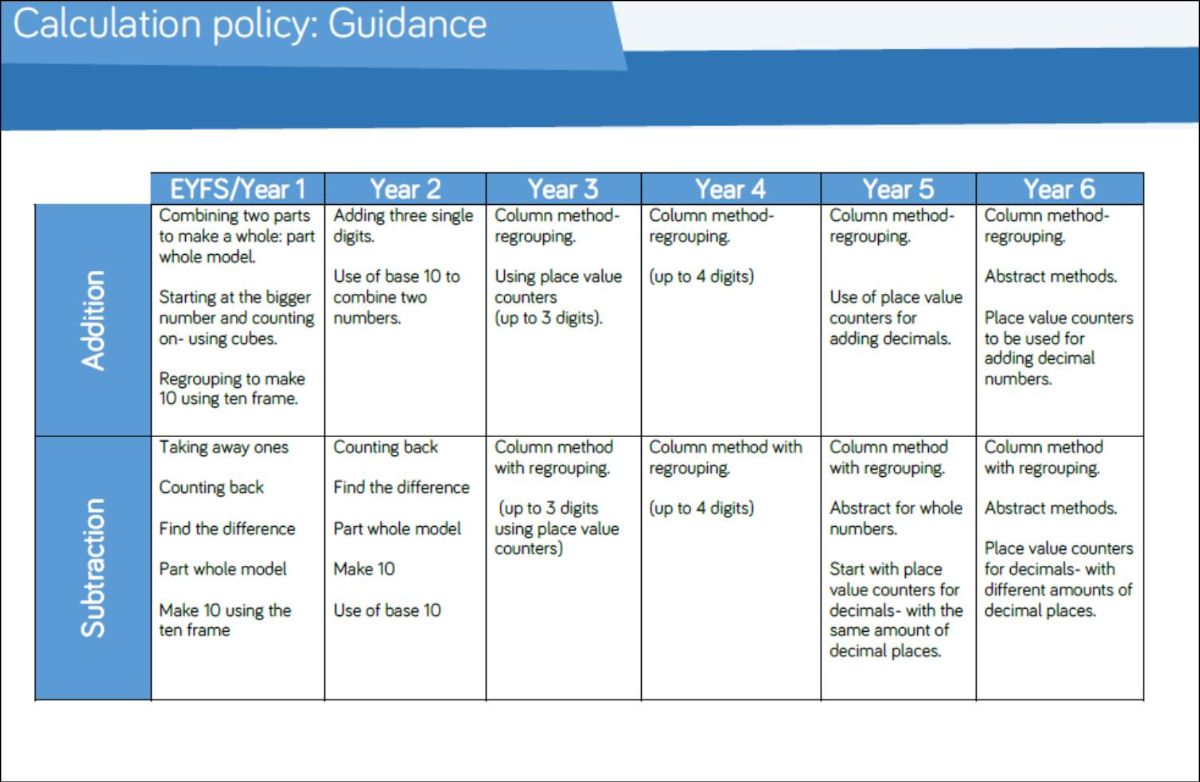
Calculation Policy - Primary / Elementary Phase
Laying the Foundations of Early Mathematics
This set of resource materials is intended to help practitioners working with children in the Early Years Foundation Stage (EYFS), and teachers working with lower Key Stage 1 children, to plan their mathematics provision and help children to secure some of the key mathematical ideas that they will use throughout the rest of their lives. The materials have a strong focus on Number, particularly counting, and the children’s developing understanding of the patterns that underpin early work within this aspect of mathematics. Download
Teaching Mathematics
Why is Jerome Bruner important to Mathematics education?
In the 1960s American psychologist Jerome Bruner (above) put forward a theory that people learn in three basic stages: by handling real objects, through pictures, and through symbols. Bruner said symbols are "clearly the most mysterious of the three." In the 1980s Singapore developed its model method based on Bruner's theory.
Implications for teaching mathematics
Some of the implications of Bruner's theory for the teaching of mathematics are:
•children's 'readiness' to learn is not linked to age (unlike Piaget's theory);
•development of language is important to concept formation;
•adults are important in structuring and supporting children's developing ideas (compare this with Piaget's theory);
•new concepts (regardless of the age of the learner) should be taught enactively, then ironically and, finally, symbolically as ways of capturing experiences in the memory;
•it is important to include practical activities and discussion as an integral part of mathematics.;
•the use of pictorial recording and the classroom environment are important.

The Times Educational Supplement is an excellent source of research articles and resources. They also have a dedicated section to support the teaching of Mastery in Mathematics. Read More
There are several organisations that have developed Mathematical Mastery at a whole school level.
Mathematical Mastery organisation have several key principles that underpin all that they do. They have high expectations for every child. They teach fewer topics in greater depth. They emphasise problem-solving and conceptual understanding. They also promote a 'Growth Mindset'.
 White Rose Maths Hub
White Rose Maths Hub
Influenced, inspired and informed by the work of leading maths researchers and practitioners across the world, White Rose Maths brings together a team of highly experienced and passionate maths teaching experts to train, guide, help and support all those who want to make change happen in their schools.
Schemes of Learning, Assessments and Mixed-age Learning Plans
White Rose always make a strong effort to keep their content advancing in line with the latest best practice and National Curriculum requirements, White Rose Maths’ latest SOL feature smaller learning steps and additional techniques to help you embed deeper learning.
All of these materials are available for you to download and use FREE.
White Rose Education | White Rose Education
White Rose Education delivers maths and science resources, CPD, tools, advice and guidance for schools, teachers and parents.

Jerome Bruner is remembered as a visionary educator who offered groundbreaking insights into how children learn.

Fluency is knowing how a number can be composed and decomposed and using that information to be flexible and efficient with solving problems.
Fosnot and Dolk (2001)

Math Library
Have a question about elementary mathematics content? Pedagogy? Language? Explore our library of posts answering questions teachers most frequently ask about elementary mathematics or ideas that they often want to investigate. These informational pages give insight and clarify concepts about elementary mathematics for teachers.
Mathematics Links for Pupils & Teachers
- Advice from Geoff Smith for young mathematicians
- Arbelos - solutions for mathematics enrichment. High quality extension and enrichment materials for secondary mathematics teachers.
- Edfinity - UKMT Skill Builders - Free, on-line, problem solving question sets for Individual Maths Challenges. Click here for the User Guide.
- Further Maths Support Programme - Supporting the teacher of Further Maths in schools and colleges.
- Maths Careers - Information about the many potential areas of employment where mathematics plays a significant role.
- Maths Inspiration - Inspiring maths events for year 11 and beyond.
- Millennium Mathematics Project - Helping people of all ages share in the excitement of mathematics.
- National Centre for Excellence in the Teaching of Mathematics - Ensuring that all teachers of maths have easy access to high quality, maths-specific continuing professional development (CPD)
- National Numeracy - useful resource list from National Numeracy.
- National STEM Centre - Working with schools, colleges and partner organisations to support STEM education
- NRICH - A highly recommended on-line Maths Club - problems, puzzles & articles galore!
Organisations Associated with UKMT
- Edinburgh Mathematical Society - The principal mathematical society for the University community in Scotland.
- EGMO - European Girls' Mathematical Olympiad - a new event for female, school-age, strong mathematicians.
- Institute of Mathematics & its Applications - The UK's learned and professional society for mathematics and its applications.
- Joint Mathematical Council of the United Kingdom - Provides co-ordination between the Constituent Societies and generally to promote the advancement of mathematics
- Leeds University - The UKMT Maths Challenges Office is based at Leeds University.
- London Mathematical Society - Various publications, meetings and conferences.
- Mathematical Association - Will be of particular interest to teachers of mathematics. Produces several publications.
- The Royal Institution - Read about the history and activities of the RI, including the famous Christmas lectures.
- The Royal Society - The independent scientific academy of the UK, dedicated to promoting excellence in science.
- Scottish Mathematical Council - Further information about mathematical activities in Scotland.
International Organisations
- AMT - Australian Mathematics Trust - Successfully running national maths competitions in Australia since 1978.
- Association Kangourou sans Frontières - Launched in Europe in 1991, now operating in over 60 countries worldwide, and named in tribute to the Australians.
- Canadian Mathematics Competition - Running since 1963 from the University of Waterloo in Ontario
- International Mathematical Olympiad (IMO) - The official world-wide IMO page.
- International Mathematical Olympiad Foundation - The charitable organization that handles donations in support of the IMO.
- South Africa - Mathematical Digest - A quarterly magazine for high school pupils in South Africa

http://www.youtube.comlistType=playlist&list=PL3723_z6WqS7Dkp9jbUTRS2qncFsVxTjH
No Title
No Description
Getting to grips... What is mastery? | Prof Ruth Merttens | Teacher training from Hamilton Trust
Professor Ruth Merttens discusses what the new National Curriculum actually means in practice. She explains how to adapt to a curriculum based on skills mastery and outlines four key areas of focus: - Memorisation - Consistent development of models and images - Constant intervention - Embedded learning Ruth provides pedagogical training across the UK.
Math Seminar | Number Sense: A Biological Look at How Our Minds Create Mathematics
By Andrea Hayes. How can an infant know that 1 plus 1 equals 2? Why is it that, even after years of school, many of us still aren't sure if 6 times 7 is 42 or 54? How can animals without a language know some elementary arithmetic?
Teaching Cambridge Primary Maths
Watch a stage three Cambridge Primary Maths lesson taking place at Eleanor Palmer Primary School, London, in the UK.
Jo Boaler Clip on number sense
Uploaded by Ali Beach on 2014-05-06.
Jo Boaler is a professor of mathematics education at Stanford and the co-founder of YouCubed. The research referred to in the video can be seen here. Read more
How you can be good at math, and other surprising facts about learning | Jo Boaler | TEDxStanford
You have probably heard people say they are just bad at math, or perhaps you yourself feel like you are not "a math person." Not so, says Stanford mathematics education professor Jo Boaler, who shares the brain research showing that with the right teaching and messages, we can all be good at math.
You have probably heard people say they are just bad at math, or perhaps you yourself feel like you are not “a math person.” Not so, says Stanford mathematics education professor Jo Boaler, who shares the brain research showing that with the right teaching and messages, we can all be good at math. Not only that, our brains operate differently when we believe in ourselves. Boaler gives hope to the the mathematically fearful or challenged, shows a pathway to success, and brings into question the very basics of how our teachers approach what should be a rewarding experience for all children and adults.
How to strengthen students' accuracy, efficiency and flexibility with mental math and computation strategies.
Presenter: Sherry Parrish, Professional Development Consultant; Assistant Professor, The University of Alabama at Birmingham
Sherry Parrish: Number Talks: Building Numerical Reasoning
How to strengthen students' accuracy, efficiency and flexibility with mental math and computation strategies Presenter: Sherry Parrish, Professional Development Consultant; Assistant Professor, The University of Alabama at Birmingham This video was filmed during Scholastic's 2014 Teacher Week.
Number Talks at UWCSEA
Number Talks at UWCSEA East are short structured sessions that develop Primary School students' understanding of numbers.
Number Talks at UWCSEA East are short structured sessions that develop Primary School students' understanding of numbers
Mastery in Mathematics
Since mastery is what we want pupils to acquire (or go on acquiring), rather than teachers to demonstrate, we use the phrase ‘teaching for mastery’ to describe the range of elements of classroom practice and school organisation that combine to give pupils the best chances of mastering mathematics.
And mastering maths means acquiring a deep, long-term, secure and adaptable understanding of the subject. At any one point in a pupil’s journey through school, achieving mastery is taken to mean acquiring a solid enough understanding of the maths that’s been taught to enable him/her move on to more advanced material.
- The essential elements of maths teaching for mastery are contained in this paper, published in June 2016
- The NCETM’s early thinking about teaching for mastery was first contained in this paper, from autumn 2014.
- The NCETM’s Director for Primary Debbie Morgan has given numerous presentations to audiences across England. This one, to a group of teachers and heads in North Lincolnshire, took place in December 2015.
- This video shows a teaching for mastery workshop in March 2016 attended by teachers and heads from Cheshire.
- Several blog posts by the NCETM’s Director Charlie Stripp deal with aspects of teaching for mastery, in the primary and secondary phases.
The materials, produced in collaboration with Oxford University Press, are divided into six separate documents, one for each of Years 1 to 6 inclusive
Mathematics
- Stage 1 Maths Curriculum Framework
- Stage 2 Maths Curriculum Framework
- Stage 3 Maths Curriculum Framework
- Stage 4 Maths Curriculum Framework
- Stage 5 Maths Curriculum Framework
- Stage 6 Maths Curriculum Framework
- Stage 7 Maths Curriculum Framework
- Stage 8 Maths Curriculum Framework
- Stage 9 Maths Curriculum Framework